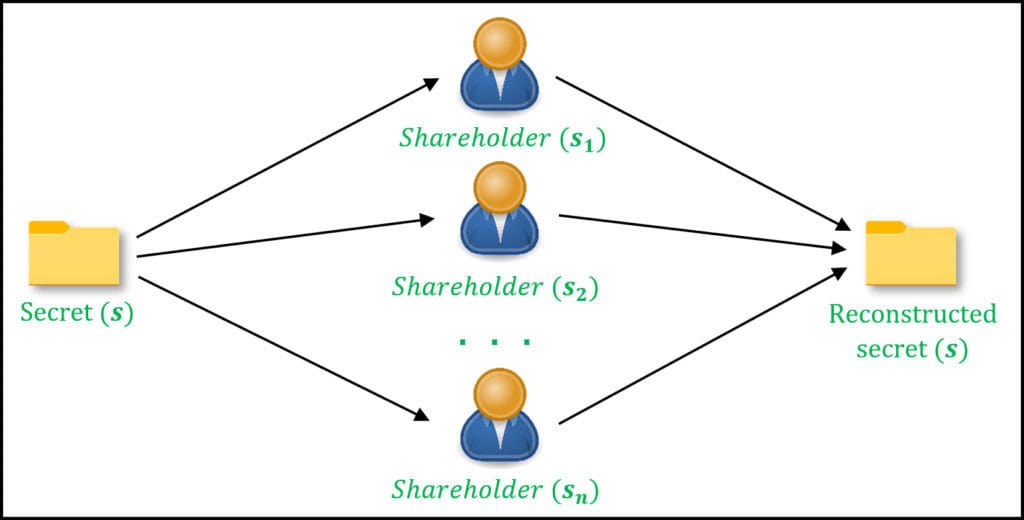
La nostra soluzione sfrutterà la condivisione segreta di Shamir per la fiducia distribuita e la crittografia omomorfica additiva per i calcoli sui dati crittografati. Alla fine, avrai un sistema backend robusto che può rilevare frodi tra più parti senza compromettere la privacy dei dati individuali.
Il Problema: Rilevamento Collaborativo delle Frodi in un Mondo Ossessionato dalla Privacy
Il rilevamento delle frodi spesso richiede il confronto di dati provenienti da più fonti. Ma nella nostra era attenta alla privacy, condividere dati grezzi è un grande no-no. Ecco dove si trova la nostra sfida:
- Diversi istituti bancari devono controllare le attività fraudolente tra le loro basi di clienti
- Nessuna delle banche vuole rivelare i dati dei propri clienti agli altri
- Dobbiamo trovare modelli fraudolenti comuni senza esporre i record individuali
Sembra di voler fare una frittata senza rompere le uova, vero? Bene, è esattamente ciò che ci permette di fare l'MPC!
La Soluzione: MPC e PSI in Soccorso
Il nostro approccio utilizzerà due principali tecniche crittografiche:
- Condivisione Segreta di Shamir (SSS): Per dividere i dati sensibili in parti
- Crittografia Omomorfica Additiva (AHE): Per eseguire calcoli su dati crittografati
Combineremo questi elementi per creare un protocollo di Intersezione Privata degli Insiemi, che ci permetterà di trovare elementi comuni tra dataset senza rivelare i dataset stessi.
Passo 1: Configurazione della Condivisione Segreta di Shamir
Per prima cosa, implementiamo la Condivisione Segreta di Shamir. Questo algoritmo ci permetterà di dividere i nostri dati sensibili in parti che possono essere distribuite tra i partecipanti.
import random
from sympy import *
def generate_polynomial(secret, degree, prime):
coefficients = [secret] + [random.randint(0, prime-1) for _ in range(degree)]
return coefficients
def evaluate_polynomial(coefficients, x, prime):
return sum(coeff * pow(x, power, prime) for power, coeff in enumerate(coefficients)) % prime
def create_shares(secret, num_shares, threshold, prime):
coefficients = generate_polynomial(secret, threshold-1, prime)
return [(i, evaluate_polynomial(coefficients, i, prime)) for i in range(1, num_shares+1)]
# Uso
prime = 2**127 - 1 # Un numero primo di Mersenne
secret = 1234
shares = create_shares(secret, num_shares=5, threshold=3, prime=prime)
print(shares)
Questa implementazione ci permette di dividere un segreto in più parti, dove qualsiasi sottoinsieme di parti (uguale o superiore alla soglia) può ricostruire il segreto, ma meno parti non rivelano nulla sul segreto.
Passo 2: Implementazione della Crittografia Omomorfica Additiva
Successivamente, implementeremo uno schema semplice di crittografia omomorfica additiva. Per questo esempio, useremo il sistema crittografico di Paillier, che consente operazioni di addizione su dati crittografati.
from phe import paillier
def generate_keypair():
return paillier.generate_paillier_keypair()
def encrypt(public_key, value):
return public_key.encrypt(value)
def decrypt(private_key, encrypted_value):
return private_key.decrypt(encrypted_value)
def add_encrypted(encrypted_a, encrypted_b):
return encrypted_a + encrypted_b
# Uso
public_key, private_key = generate_keypair()
a, b = 10, 20
encrypted_a = encrypt(public_key, a)
encrypted_b = encrypt(public_key, b)
encrypted_sum = add_encrypted(encrypted_a, encrypted_b)
decrypted_sum = decrypt(private_key, encrypted_sum)
print(f"Somma decrittata: {decrypted_sum}") # Dovrebbe essere 30
Questo schema di crittografia omomorfica ci permette di eseguire addizioni su valori crittografati senza decrittarli prima.
Passo 3: Implementazione dell'Intersezione Privata degli Insiemi
Ora, combiniamo SSS e AHE per creare il nostro protocollo di Intersezione Privata degli Insiemi:
def private_set_intersection(set_a, set_b, threshold, prime):
public_key, private_key = generate_keypair()
# Creare parti per ogni elemento in set_a
shares_a = {elem: create_shares(elem, len(set_b), threshold, prime) for elem in set_a}
# Crittografare le parti
encrypted_shares_a = {elem: [encrypt(public_key, share[1]) for share in shares] for elem, shares in shares_a.items()}
# Simulare l'invio di parti crittografate all'altra parte
# In uno scenario reale, questo comporterebbe la comunicazione di rete
# L'altra parte valuta il proprio set rispetto alle parti ricevute
intersection = set()
for elem_b in set_b:
possible_match = True
for elem_a, enc_shares in encrypted_shares_a.items():
reconstructed = sum(share * pow(elem_b, i+1, prime) for i, share in enumerate(enc_shares))
if decrypt(private_key, reconstructed) != 0:
possible_match = False
break
if possible_match:
intersection.add(elem_b)
return intersection
# Uso
set_a = {1, 2, 3, 4, 5}
set_b = {3, 4, 5, 6, 7}
threshold = 3
prime = 2**127 - 1
intersection = private_set_intersection(set_a, set_b, threshold, prime)
print(f"Intersezione: {intersection}")
Questa implementazione permette a due parti di trovare l'intersezione dei loro insiemi senza rivelare gli insiemi stessi.
Mettere Tutto Insieme: Sistema di Rilevamento delle Frodi
Ora che abbiamo i nostri elementi costitutivi, creiamo un semplice sistema di rilevamento delle frodi utilizzando la nostra Intersezione Privata degli Insiemi basata su MPC:
class Bank:
def __init__(self, name, suspicious_accounts):
self.name = name
self.suspicious_accounts = set(suspicious_accounts)
class FraudDetectionSystem:
def __init__(self, banks, threshold, prime):
self.banks = banks
self.threshold = threshold
self.prime = prime
def detect_common_suspicious_accounts(self):
if len(self.banks) < 2:
return set()
common_suspicious = self.banks[0].suspicious_accounts
for i in range(1, len(self.banks)):
common_suspicious = private_set_intersection(
common_suspicious,
self.banks[i].suspicious_accounts,
self.threshold,
self.prime
)
return common_suspicious
# Uso
bank_a = Bank("Banca A", [1001, 1002, 1003, 1004, 1005])
bank_b = Bank("Banca B", [1003, 1004, 1005, 1006, 1007])
bank_c = Bank("Banca C", [1005, 1006, 1007, 1008, 1009])
fraud_system = FraudDetectionSystem([bank_a, bank_b, bank_c], threshold=3, prime=2**127 - 1)
common_suspicious = fraud_system.detect_common_suspicious_accounts()
print(f"Conti sospetti comuni: {common_suspicious}")
Questo sistema permette a più banche di rilevare collaborativamente potenziali conti fraudolenti senza rivelare le loro liste individuali di conti sospetti.
Spunti di Riflessione: Implicazioni e Considerazioni
Prima di correre a implementare questo in produzione, ecco alcune cose su cui riflettere:
- Prestazioni: I protocolli MPC possono essere computazionalmente intensivi. Come ottimizzeresti questo per grandi dataset?
- Comunicazione di Rete: Il nostro esempio presuppone un calcolo locale. In realtà, dovresti gestire la comunicazione di rete sicura tra le parti.
- Modello di Sicurezza: La nostra implementazione presuppone parti semi-oneste. Quali cambiamenti sarebbero necessari per avversari malevoli?
- Conformità Normativa: Come si allinea questo approccio con le normative sulla protezione dei dati come GDPR o CCPA?
Conclusione: Il Potere del Calcolo che Preserva la Privacy
Abbiamo appena scalfito la superficie di ciò che è possibile con il Calcolo Multi-Party Sicuro e l'Intersezione Privata degli Insiemi. Sfruttando queste tecniche, possiamo creare potenti sistemi collaborativi che rispettano la privacy individuale.
Ricorda, nel mondo della privacy dei dati, non stiamo solo scrivendo codice – stiamo costruendo fiducia. Quindi, la prossima volta che qualcuno ti dice che privacy e utilità dei dati sono mutuamente esclusive, puoi dire con sicurezza: "Tieni la mia birra crittografata omomorficamente!"
Buona programmazione, e che i tuoi calcoli siano sempre sicuri!
"In Dio confidiamo. Tutti gli altri devono portare dati." - E ora, grazie all'MPC, possono portare dati senza effettivamente portarli!