Di cosa stiamo parlando in nome di Évariste Galois?
Prima di addentrarci nel mondo della crittografia, cerchiamo di capire cosa sono effettivamente i campi di Galois. Prendono il nome dal giovane matematico francese Évariste Galois (che, curiosità, morì in un duello a 20 anni - un'uscita di scena davvero drammatica), questi campi sono insiemi finiti di elementi con proprietà algebriche speciali.
In parole più semplici, immagina un parco giochi dove i numeri seguono regole molto specifiche. Queste regole garantiscono che, indipendentemente da come sommi, sottrai, moltiplichi o dividi questi numeri (tranne per zero, perché anche in matematica non possiamo dividere per zero), finisci sempre con un altro numero nello stesso parco giochi.
La Connessione Crittografica: Perché i Campi di Galois Sono Importanti
Ora potresti pensare, "Bella storia, ma cosa c'entra con la sicurezza dei miei meme di gatti?" Ottima domanda! I campi di Galois sono la spina dorsale di diversi sistemi crittografici meno conosciuti ma sempre più importanti. Ecco perché stanno suscitando tanto interesse:
- Efficienza: Le operazioni nei campi di Galois possono essere incredibilmente veloci ed efficienti, il che è cruciale per la crittografia in tempo reale.
- Resilienza: Offrono una forte resistenza contro certi tipi di attacchi crittografici.
- Flessibilità: I campi di Galois di diverse dimensioni possono essere utilizzati per creare vari livelli di sicurezza, rendendoli adattabili a diverse esigenze.
Campi di Galois in Azione: Sistemi Crittografici nel Mondo Reale
Vediamo alcuni sistemi crittografici che utilizzano i campi di Galois:
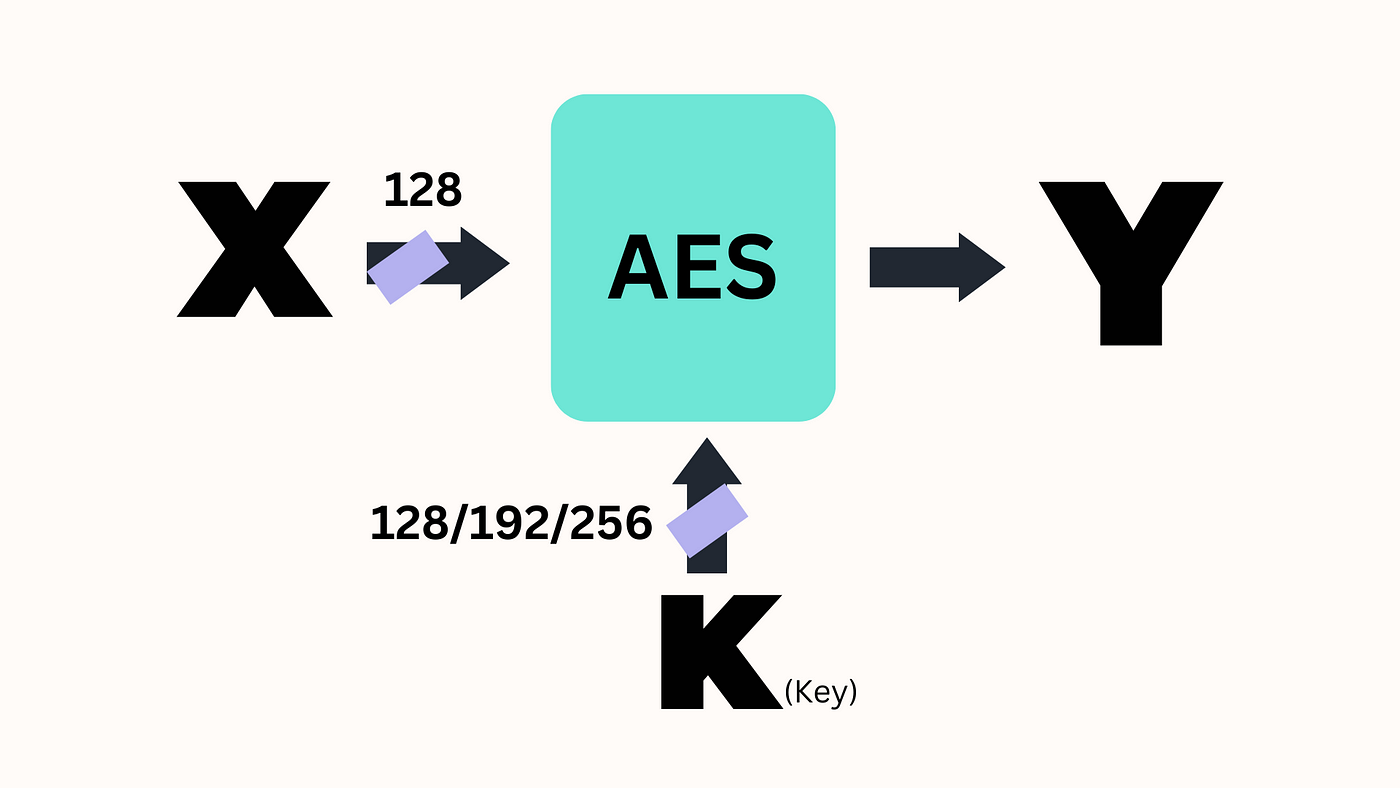
1. Advanced Encryption Standard (AES)
Sì, proprio quell'AES. Anche se non è esattamente "di nuova generazione", l'AES utilizza operazioni nel campo di Galois GF(2^8) per il suo passaggio MixColumns. Questo aiuta a creare la confusione e la diffusione necessarie per una crittografia sicura.
2. Correzione degli Errori di Reed-Solomon
Anche se utilizzati principalmente per la correzione degli errori nella trasmissione e archiviazione dei dati, i codici Reed-Solomon, basati sull'aritmetica dei campi di Galois, hanno anche applicazioni in crittografia, in particolare nei sistemi di condivisione segreta.
3. Crittografia a Curve Ellittiche (ECC)
L'ECC opera su campi finiti, spesso campi di Galois. Questo permette di avere chiavi di dimensioni più piccole rispetto all'RSA mantenendo livelli di sicurezza equivalenti.
La Prossima Frontiera: Crittografia Post-Quantistica
Qui le cose diventano davvero interessanti. Con i computer quantistici all'orizzonte, che minacciano di rompere molti dei nostri metodi di crittografia attuali, i crittografi stanno guardando ai campi di Galois per sviluppare algoritmi resistenti ai quanti.
Crittografia Basata su Codici
Un'area promettente è la crittografia basata su codici, che si basa fortemente sulle operazioni nei campi di Galois. Il sistema crittografico McEliece, ad esempio, utilizza codici di correzione degli errori su campi finiti per creare un sistema di crittografia a chiave pubblica che si ritiene resistente ai quanti.
Ecco un esempio semplificato di come un campo di Galois potrebbe essere utilizzato nella crittografia basata su codici:
import galois
# Crea un campo di Galois di dimensione 2^8
GF = galois.GF(2**8)
# Genera un messaggio casuale
message = GF.Random(10)
# Genera un vettore di errore casuale
error = GF.Random(10)
# Simula la codifica e l'aggiunta di errore
encoded_message = message + error
# In realtà, la decodifica coinvolgerebbe algoritmi complessi
# utilizzando le proprietà del campo di Galois
decoded_message = encoded_message - error
print(f"Messaggio originale: {message}")
print(f"Messaggio decodificato: {decoded_message}")
print(f"Sono uguali? {all(message == decoded_message)}")
Questo è, ovviamente, un esempio molto semplificato. I veri sistemi crittografici basati su codici coinvolgono operazioni molto più complesse e campi di dimensioni maggiori.
Sfide e Considerazioni
Prima di riscrivere tutto il tuo codice crittografico con i campi di Galois, consideriamo alcune sfide:
- Complessità: Lavorare con i campi di Galois richiede una solida comprensione dell'algebra astratta. Non è per i deboli di cuore (o di matematica).
- Implementazione: L'implementazione efficiente dell'aritmetica dei campi di Galois può essere complicata, specialmente su hardware non ottimizzato per queste operazioni.
- Standardizzazione: Molti sistemi crittografici basati su campi di Galois sono ancora in fase di ricerca e non sono ancora stati ampiamente standardizzati.
Allora, Qual è il Grande Problema?
I campi di Galois sono più di una semplice curiosità matematica. Stanno fornendo la base per una nuova generazione di sistemi crittografici che promettono di essere più veloci, più efficienti e potenzialmente resistenti ai quanti. Mentre ci muoviamo verso un'era in cui la sicurezza dei dati è più critica che mai, queste strutture matematiche probabilmente giocheranno un ruolo sempre più importante nel mantenere al sicuro le nostre vite digitali.
Che tu sia un appassionato di crittografia, un professionista della sicurezza o semplicemente qualcuno che vuole sembrare intelligente alle feste, capire il ruolo dei campi di Galois nella crittografia moderna vale sicuramente il tuo tempo. Chissà? La prossima svolta nella sicurezza dei dati potrebbe provenire proprio da questi campi finiti di infinite possibilità.
"L'arte di fare matematica consiste nel trovare quel caso speciale che contiene tutti i germi della generalità." - David Hilbert
E nel caso della crittografia moderna, quel caso speciale potrebbero essere i campi di Galois. Quindi la prossima volta che qualcuno ti chiede del futuro della crittografia, puoi dire con sicurezza: "È tutto sui Galois, sui Galois, nessun problema."
Ulteriori Letture
Se sei incuriosito e vuoi approfondire il mondo dei campi di Galois e le loro applicazioni nella crittografia, ecco alcune risorse per iniziare:
- Galois: Una libreria Python 3 per l'aritmetica dei campi di Galois
- Rapporto NIST sulla Crittografia Post-Quantistica
- Manuale di Crittografia a Curve Ellittiche e Iperellittiche
Ricorda, nel mondo della crittografia, l'avanguardia di oggi è l'obsoleto di domani. Rimani curioso, continua a imparare e chissà? Potresti essere tu a scoprire la prossima grande novità nella crittografia. Che i Galois siano con te!