La notazione Big O non è solo un gergo accademico: è la tua arma segreta per capire come si comporta il tuo codice quando le dimensioni dell'input crescono. Immagina di costruire la prossima grande app di social media. Il tuo algoritmo funziona bene con 100 utenti, ma cosa succede quando raggiungi 1 milione? È qui che entra in gioco la Big O.
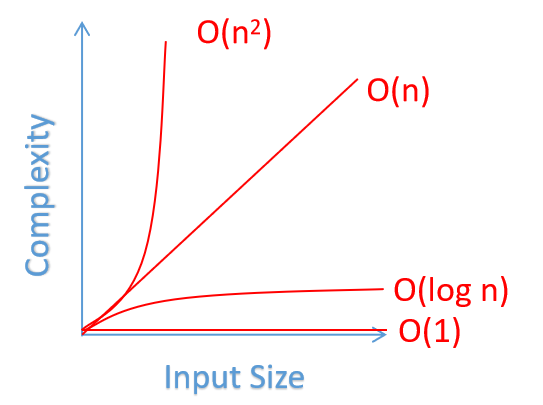
Alla base, Big O descrive il limite superiore del tasso di crescita di un algoritmo. Risponde alla domanda: "Come scala il tempo di esecuzione o l'uso dello spazio quando aumenta la dimensione dell'input?" Analizziamo le classi di complessità più comuni:
- O(1): Tempo costante. L'algoritmo impiega lo stesso tempo indipendentemente dalla dimensione dell'input. È il santo graal dell'efficienza.
- O(log n): Tempo logaritmico. Efficiente per grandi set di dati, spesso visto negli algoritmi di ricerca binaria.
- O(n): Tempo lineare. Il tempo di esecuzione cresce direttamente con la dimensione dell'input. Comune nelle iterazioni semplici.
- O(n log n): Tempo linearitmico. Tipico per algoritmi di ordinamento efficienti come il mergesort.
- O(n^2): Tempo quadratico. Spesso visto nei cicli annidati. Può diventare problematico per input di grandi dimensioni.
- O(2^n): Tempo esponenziale. L'algoritmo raddoppia il suo tempo di esecuzione con ogni input aggiuntivo. Evitalo se possibile!
Dalla Teoria alla Pratica: Analizzare Codice Reale
Indossiamo i nostri cappelli da detective e analizziamo un po' di codice. Considera queste due funzioni che trovano il valore massimo in un array:
def find_max_naive(arr):
max_val = arr[0]
for i in range(len(arr)):
for j in range(len(arr)):
if arr[j] > max_val:
max_val = arr[j]
return max_val
def find_max_optimized(arr):
return max(arr)
A prima vista, entrambe le funzioni fanno il loro lavoro. Ma analizziamole:
find_max_naiveha cicli annidati, dandogli una complessità di O(n^2). Ahi!find_max_optimizedutilizza la funzionemax()integrata di Python, che funziona in tempo O(n).
La differenza? Per un array di 1.000.000 elementi, l'approccio ingenuo potrebbe richiedere ore, mentre la versione ottimizzata termina in millisecondi. Questa è la potenza della comprensione della Big O!
Tempo vs. Spazio: Il Dilemma Eterno
Quando ottimizziamo gli algoritmi, spesso affrontiamo un dilemma classico: diamo priorità alla velocità (complessità temporale) o all'uso della memoria (complessità spaziale)? Considera questo esempio di calcolo dei numeri di Fibonacci:
def fib_recursive(n):
if n <= 1:
return n
return fib_recursive(n-1) + fib_recursive(n-2)
def fib_dynamic(n):
fib = [0, 1]
for i in range(2, n+1):
fib.append(fib[i-1] + fib[i-2])
return fib[n]
La versione ricorsiva (fib_recursive) ha una complessità temporale di O(2^n) ma utilizza uno spazio extra minimo. L'approccio di programmazione dinamica (fib_dynamic) scambia spazio per tempo, raggiungendo una complessità temporale di O(n) al costo di O(n) spazio.
Ricorda: Non esiste una soluzione valida per tutti. Il miglior approccio dipende dai tuoi vincoli e requisiti specifici.
Sconfiggere il Drago O(n^2): Strategie di Ottimizzazione
Hai incontrato un algoritmo O(n^2) nel tuo codice? Non farti prendere dal panico! Ecco alcune strategie per domare quella bestia quadratica:
- Usa strutture dati appropriate: Gli HashMap possono trasformare cicli annidati in passaggi singoli.
- Dividi e conquista: Tecniche come la ricerca binaria possono ridurre drasticamente la complessità.
- Caching e memoizzazione: Memorizza i risultati per evitare calcoli ridondanti.
- Tecnica dei due puntatori: Utile per problemi di array, spesso riducendo O(n^2) a O(n).
Vediamo un esempio di ottimizzazione di una funzione che trova coppie in un array con una somma data:
# Soluzione O(n^2)
def find_pairs_naive(arr, target_sum):
pairs = []
for i in range(len(arr)):
for j in range(i+1, len(arr)):
if arr[i] + arr[j] == target_sum:
pairs.append((arr[i], arr[j]))
return pairs
# Soluzione O(n)
def find_pairs_optimized(arr, target_sum):
seen = set()
pairs = []
for num in arr:
complement = target_sum - num
if complement in seen:
pairs.append((num, complement))
seen.add(num)
return pairs
La versione ottimizzata utilizza un HashSet per ottenere una complessità temporale lineare. Per array di grandi dimensioni, questo può fare la differenza tra aspettare secondi o millisecondi.
Strumenti del Mestiere: Profilazione e Analisi
La teoria è fantastica, ma a volte hai bisogno di dati concreti. Ecco alcuni strumenti per aiutarti ad analizzare le prestazioni del tuo codice:
- Modulo timeit di Python: Ottimo per benchmark rapidi.
- cProfile: Fornisce un'analisi dettagliata delle prestazioni per il codice Python.
- memory_profiler: Aiuta a monitorare l'uso della memoria negli script Python.
- Big O Cheat Sheet: Un utile riferimento per algoritmi e strutture dati comuni.
Consiglio da professionista: Molti IDE, come PyCharm, dispongono di strumenti di profilazione integrati. Usali!
Best Practices per l'Ottimizzazione degli Algoritmi
- Misura, non indovinare: Profilare sempre il tuo codice prima di ottimizzare.
- Conosci i tuoi dati: Comprendere il tuo input può portare a ottimizzazioni su misura.
- Usa funzioni integrate: Sono spesso altamente ottimizzate.
- Sii pigro: Rimanda i calcoli finché non sono assolutamente necessari.
- Mantienilo semplice: A volte, un algoritmo semplice è migliore di uno "ottimizzato" complesso.
Conclusione: La Grande Immagine della Big O
Comprendere la Big O non riguarda solo la scrittura di codice più veloce, ma anche la scrittura di codice più intelligente. Ti aiuta a prendere decisioni informate, prevedere problemi di scalabilità e comunicare efficacemente sulle prestazioni.
Ricorda, l'ottimizzazione prematura è la radice di tutti i mali (o almeno così si dice). Inizia sempre scrivendo codice pulito e corretto. Poi, se le prestazioni sono un problema, usa i tuoi nuovi superpoteri Big O per ottimizzare dove conta di più.
Ora vai avanti e conquista quegli algoritmi! Il tuo futuro te stesso (e i tuoi utenti) ti ringrazieranno.
"La prima regola dell'ottimizzazione è: non farlo. La seconda regola dell'ottimizzazione (solo per esperti) è: non farlo ancora." - Michael A. Jackson
Buona programmazione, e che i tuoi algoritmi funzionino sempre in tempo O(1)! 🚀